0. 前回の復習
標準偏差の統計的な解釈:
- 値が大きいほど、数字の集まりがバラついている。
- 値が小さいほど、数字の集まりがバラついていない。
- すべての数字が同じ値のとき、0を示す。
- したがって、標準偏差の最小値は0となる。
品質管理への適用:
- 同じ製品を生産する生産現場では、製品の長さや重さはバラついているとまずい。
- 標準偏差を用いることで、どれくらいバラついているのか、客観的に示すことができる。
1. ガウス性・正規性
世の中には色々な数字であふれている。例えば、この教室内に60人くらいの人間がいるとすると、以下のような数字の集まりがある。
- 60人分の身長
- 60人分の体重
- 60人分の財布に入っているお金
- 60人分のスマホの重さ
- …など
このような数字集まりにおいて、
- 平均値に近い値が多そう。
- 平均値から離れるごとに、その数値は少なくなりそう。
ということはなんとなく想像がつくと思う。この関係を確率的に定式化した性質として、ガウス性(正規性ともいう)というものがある。ガウス性を前提とすると、以下の性質が得られる。
- 「平均 – 1 × 標準偏差」〜「平均 + 1 × 標準偏差」の間に68.27%の確率でデータが発生
- 「平均 – 2 × 標準偏差」〜「平均 + 2 × 標準偏差」の間に95.45%の確率でデータが発生
- 「平均 – 3 × 標準偏差」〜「平均 + 3 × 標準偏差」の間に99.73%の確率でデータが発生
例題:
ちょっとわかりにくいので、具体例として考えてみる。
- ある村に2000人の人間が住んでいる。
- その村の平均寿命は60歳で、標準偏差は10歳であった。
- 今、目の前に一人の人間がいる(20歳くらい)。
- ガウス性を前提とすると、以下の確率はどうなるか?
- この人間が50歳〜70歳で亡くなる確率
- この人間が40歳〜80歳で亡くなる確率
- この人間が30歳〜90歳で亡くなる確率
- 選択肢: (A)32.78%, (B)59.39%, (C)68.27%, (D)95.45%, (E)99.73%
ここでわかるように、平均値と標準偏差が明らかであれば、ガウス性という前提に従うことで、確率(可能性)が求められる。あらゆる事象がガウス性に従うわけではないので注意が必要だが、多くの自然現象がガウス性に近似されることが知られている。
慣れてくると、平均と標準偏差を見た瞬間に「7割くらいの確率でxxxになりそうだな」というのが頭をよぎるようになる。もうちょっと踏み込んでいうと、製品の品質を管理したい人が、平均と標準偏差を計算するだけで「99%の確率でこの範囲の製品しか出てこない」みたいなことがわかるので、ガウス性を前提とした解釈は、それなりに利点がある。
2. 今日の問題
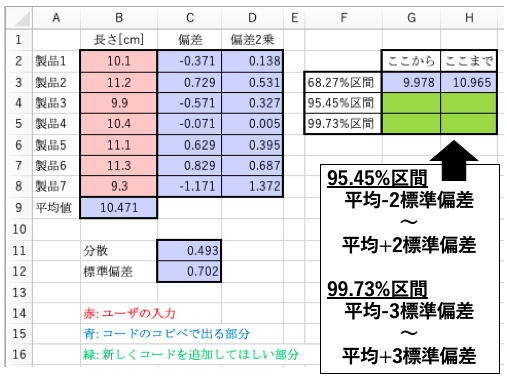
以下のコードは、7つの製品の長さに対して、その平均値と標準偏差を求め、「平均 – 1 × 標準偏差」〜「平均 + 1 × 標準偏差」の値を算出するコードである。
Private Sub CommandButton1_Click()
Dim A(7) As Double
Dim Dif(7) As Double
Dim Dif2(7) As Double
For i = 1 To 7
A(i) = Cells(i + 1, 2)
Next i
s = A(1) + A(2) + A(3) + A(4) + A(5) + A(6) + A(7)
s = s / 7
Cells(9, 2) = s ' <- 平均値
For i = 1 To 7
Dif(i) = s - A(i)
Cells(i + 1, 3) = Dif(i)
Next i
For i = 1 To 7
Dif2(i) = Dif(i) * Dif(i)
Cells(i + 1, 4) = Dif2(i)
Next i
d = Dif2(1) + Dif2(2) + Dif2(3) + Dif2(4) + Dif2(5) + Dif2(6) + Dif2(7)
d = d / 7
Cells(11, 3) = d
st = Sqr(d)
Cells(12, 3) = st ' <- 標準偏差
'平均-標準偏差 ~ 平均+標準偏差の書き込み
Cells(3, 7) = s - 1 * st
Cells(3, 8) = s + 1 * st
End Sub
- 「平均 - 2 × 標準偏差」〜「平均 + 2 × 標準偏差」を記述するコードを記載せよ(紙に書くのは、該当箇所のコードのみで良い)。
- 「平均 - 3 × 標準偏差」〜「平均 + 3 × 標準偏差」を記述するコードを記載せよ(紙に書くのは、該当箇所のコードのみで良い)。
- 適当に7個の製品の長さの数字を入れて、平均、標準偏差、「平均 - 2 × 標準偏差」〜「平均 + 2 × 標準偏差」、「平均 - 3 × 標準偏差」〜「平均 + 3 × 標準偏差」の出力を確認せよ。
3. 応用問題
「平均 - 1 × 標準偏差」〜「平均 + 1 × 標準偏差」の間に68.27%の確率でデータが発生するという性質は、如何にして算出できるか。その計算過程をすべて書き、説明せよ。
この問題はちょっと難しいので、将来、統計でばりばりやりたい人だけ取り組んでください。もしできた人は、いつでもいいので、30号館509室(大前の研究室)にきて、ホワイトボードで書きながら説明してください。完全に理解している場合、間違ってるけど頑張ってそうな場合は何点か加点します。