はじめに
新型コロナの影響で、国内外問わず様々な問題が起きています。特に国内においては、2020年4月7日に緊急事態宣言が発令され、大規模な外出自粛を要求されることになりました。外出自粛がどのような効果を持つのかわかりにくいという意見もありますので、外出自粛がどのような効果を有するか、マルチエージェントシミュレーション(MAS)環境において、検証してみたいと思います。医学の知識はほぼないので、参考程度に見てもらえると助かります。レイアウトの都合上、スマホで見ると相当見にくいと思うので、大きい画面での閲覧をオススメします。なお、本件で共同研究などをご希望される場合は、随時ご連絡ください。
履歴:
- 2020.04.17: 初版を公開しました。
マルチエージェントシミュレータについて:
普通の論文ですと理論から説明しますが、文章が続くと読みたくなくなると思うので、シミュレータの実行動画を示します。今回は外出自粛の効果を検証したいので、した場合としない場合の動画を示します。
外出自粛をしなかった場合:
外出自粛をした場合(15日から外出自粛を開始):
小規模な人口社会(人口: 1650名)を構築しました。シミュレーション期間は40日間で、1つ目の動画は外出自粛なし、2つ目の動画は外出自粛ありとしました。エージェントには3種類の人間(会社員、主婦/主夫、学生)がおり、会社員は会社へ、主婦/主夫はお店へ、学生は学校へ、毎日通うという構造をしています。1650名の中で、10名、感染者を登録してあります。動画左側、●が会社員、▼が主婦/主夫、■が学生を表します。お家から出かける時間、会社/お店/学校での滞在時刻などは、正規分布/一様分布に従う乱数で生成しています。自宅から会社/お店/学校への移動は、ユークリッド距離が最小になる経路、つまりまっすぐ移動します。
本研究では、SEIRモデルを使用しています。このモデルでは感染者の状態を、
- S: 健康(健康であるものの、免疫がないので感染する可能性がある者)
- E: 潜伏(発症はしていないがウイルスに感染し、潜伏期間である者)
- I: 発症(ウイルスの潜伏が終わり、発症した者)
- R: 回復(免疫を獲得し、再度感染はしない)
- D: 死亡(発症後、回復できずに死亡)*: 通常のモデルでは、RとDを同一視する場合もあります。
と分類します(文字色は動画左のマーカ色と対応)。感染者が誰かに感染させるのは、I状態のときのみとなります。動画では、中央右上あたりにそれぞれの状態が何人いるか、示されています。S状態からE状態へは、I状態の人と接触したときに、確率で遷移します。E状態からI状態、E状態からR/D状態への遷移は、日数経過により遷移します。
健康、潜伏、回復の状態のときは普通に動き回ることになりますが、I状態(発症)のときは、心配な人は病気を疑うので、ある確率に基づき病院に行くことになります。このとき、病床が余っていれば入院します。病床が余っていなければ、入院できないことになります。病気なのにベッドが足りず入院できないというのが医療崩壊の一つと考えられるので、このような仕組みを用意してあります。この状況を、動画の右上あたりに残っている/使用中の病床数、にて示しています。また、死亡する確率も、入院をしている方が、していない場合よりも、低くしてあります。したがって、死者を減らすには満床にさせないことが重要になります。動画上の方には、医療崩壊の目安として、入院を断られた回数も表示しています(この値は、1日が切り替わるタイミングでその日の総数を表示しています)。なお、もし入院しておらず、I状態の場合は、自分はもしかすると病気なのではと考え、外出する確率が減少します。
さて、都道府県の知事や政府は「お家にいてください! Stay home!」と必死に呼びかけています。そのため、お家にいる割合(自宅在宅割合)もグラフで示すことにしました。これは、動画の中央右下に載せてあります。下の動画にある「外出自粛をした場合」のシミュレーションは、0〜14日までは普通に過ごし、15日〜40日はあまり外出をしないような構造をしています。
動画上の方に実効再生産数という言葉があります。これは、1人の感染者が発症期間中に合計何人に感染させたかを表す数字です。I状態からR/D状態に遷移した瞬間に算出可能になる数値ですので、若干ラグがあるのと、複数人算出対象者がいる場合もあるので、平均値を示しています。本シミュレータでは、1日が切り替わるタイミングでその日の値を算出しています。実効再生産数は感染拡大・収束の指標に用いられます。実効再生産数が1未満ならば収束傾向、1より大きいならば拡大傾向であることを意味します。実効再生産数を監視しながら、1を下回るような政策を取ることが必要になります。
以上がMASの条件とシミュレーション動画の見方です。細かいパラメータなどは、本ページの下の方に載せてあります。
結果と考察
健康・潜伏・発症・回復・死亡の時系列変動
エージェントの状態についての時系列的な変化を示します。上下のグラフは、縦軸のスケールを調整した同じ結果を示しています。また、左右で縦軸のスケールが同じですので、普通に比較してokです。
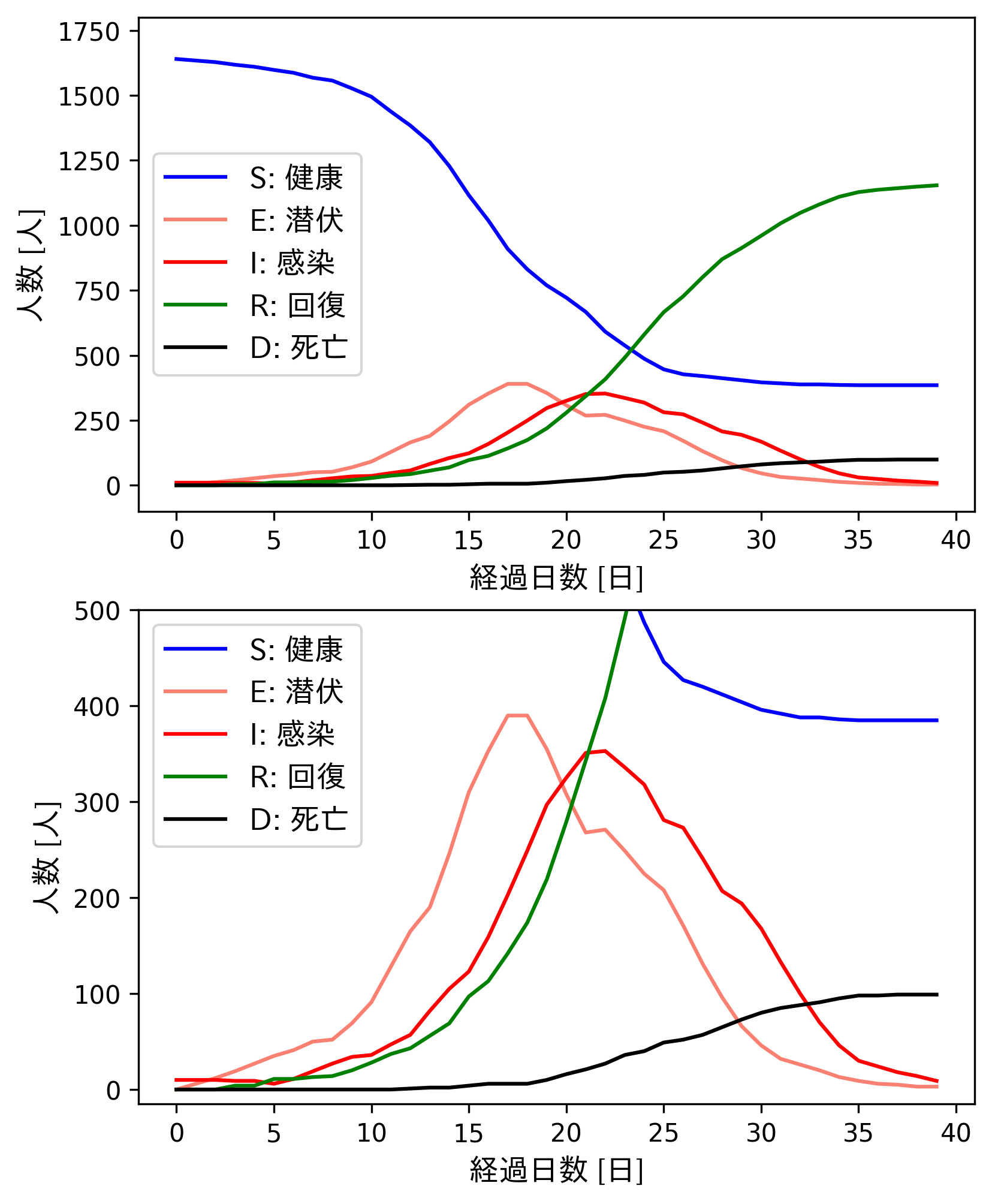
外出を自粛しない、すなわち、自然な営みを続けた場合は、シミュレーション終了時点で、死亡者が99人となりました。回復者は1200人程度いますので、全人口の7割程度が感染してしまったことを意味します。ただし、感染者が増え続けると思いきや、21日目に感染者がピークとなり、それ以降は減衰していくことも確認できます。これは、人間がウイルスに打ち勝ったということではなく、ただ単にほとんどの人が感染し免疫獲得をしたため、新規の感染者が生まれにくくなったことが原因です。つまりパンデミックとは、免疫をつけたものが二度と感染しないタイプのウイルスであれば、自然に収束します。しかし、死者がおよそ100人と、全人口の6%程度が亡くなってしまったことがわかります。なかなか受け入れがたい結果と言えるでしょう。
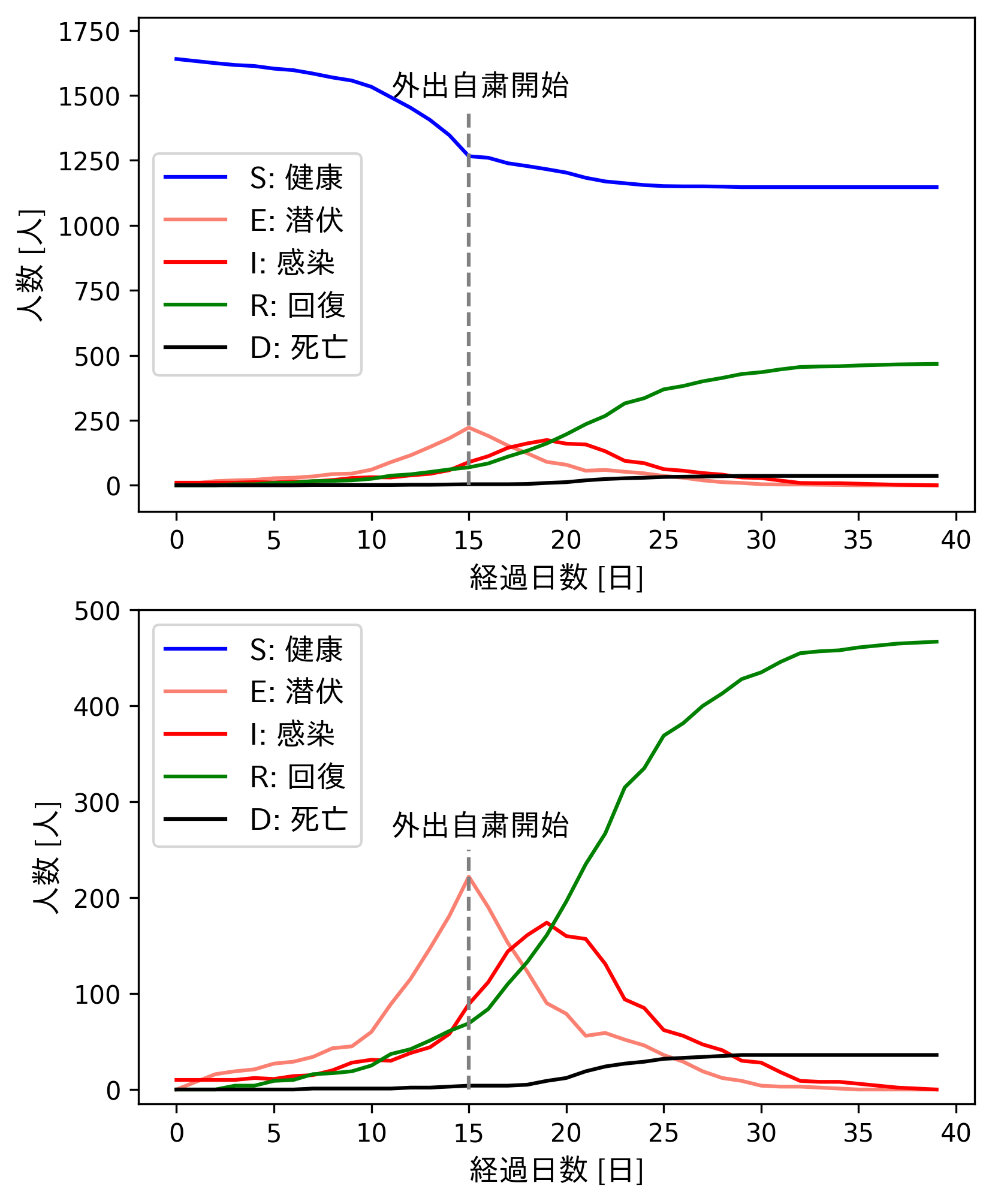
シミュレーション終了時点で、死亡者が36人となりました。グラフを見ると外出自粛をしていない15日まではぐんぐんと潜伏者・感染者が増加していきますが、自粛を開始した15日目からは、潜伏者が減少に転じています。一方、感染者については5日程度遅れた20日目付近から減少が確認できます。このように、感染者の減少にはややタイムラグがあるので、注意が必要です。いずれにせよ、外出自粛の発令をみんなできちんと守った場合は、少ない死者で感染を収束させることが可能になります。今回のシミュレーション結果では、外出自粛と比べ、70名程度(3割くらい)死亡者を減らせることがわかりました。
実効再生産数の時系列変動
感染者1人が、回復/死亡するまでに別の人に感染させた数(感染拡大・縮小の指標)。効再生産数が1未満ならば収束傾向、1より大きいならば拡大傾向であることを意味します。なんらかの介入により、1を下回らせるような仕組みを導入する必要があります。
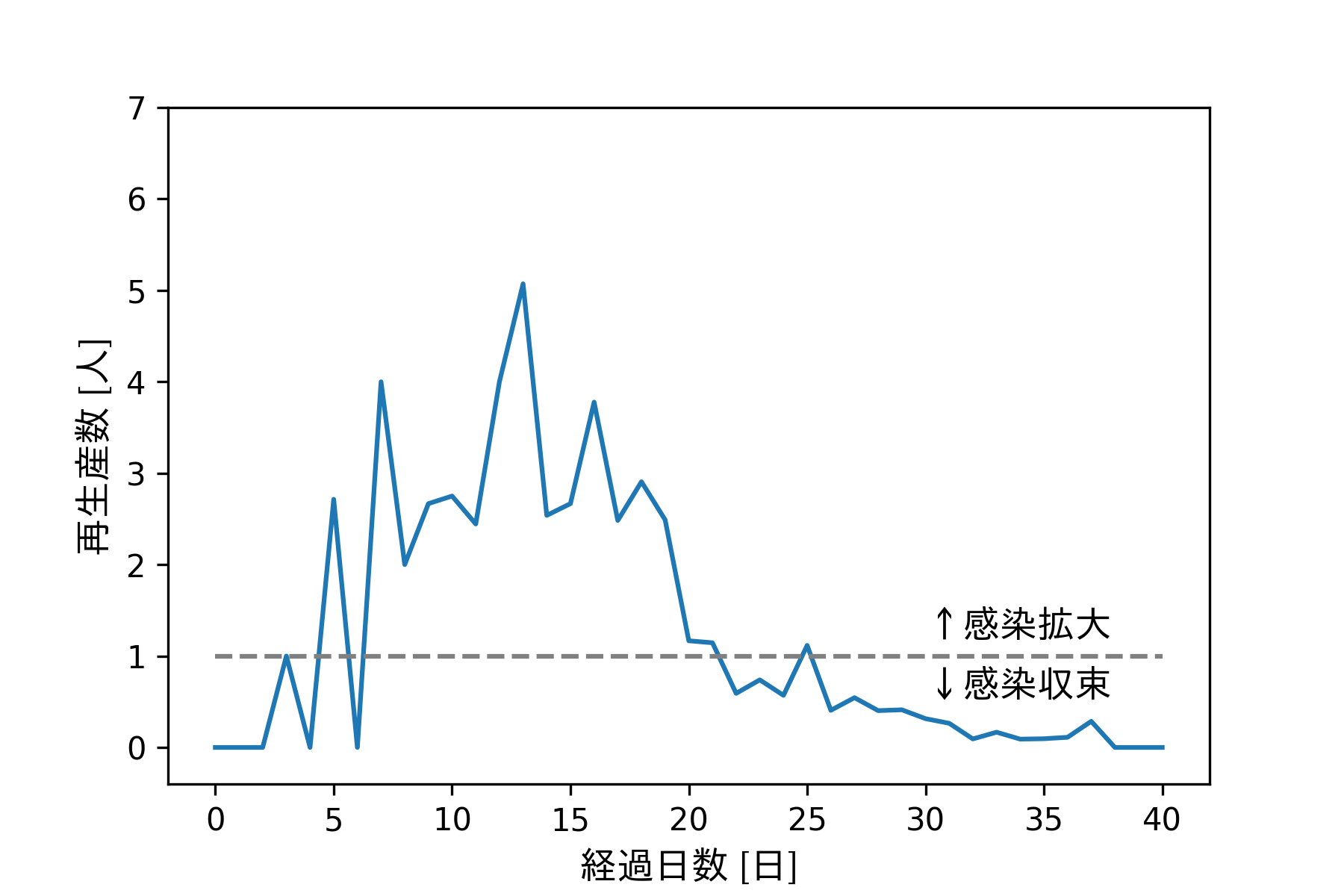
21日目までは、実効再生産数は1を超えています。一方それ以降は、1.0を超える日もありますが、次第に0に向かっていきます。すなわち、21日にて感染拡大が収束に切り替わったことを意味しています。この理由は、健康(I状態)な人が少なくなり、免疫を有する回復者(R状態)が増えることにより、新規感染が生み出されにくくなったことに由来します。
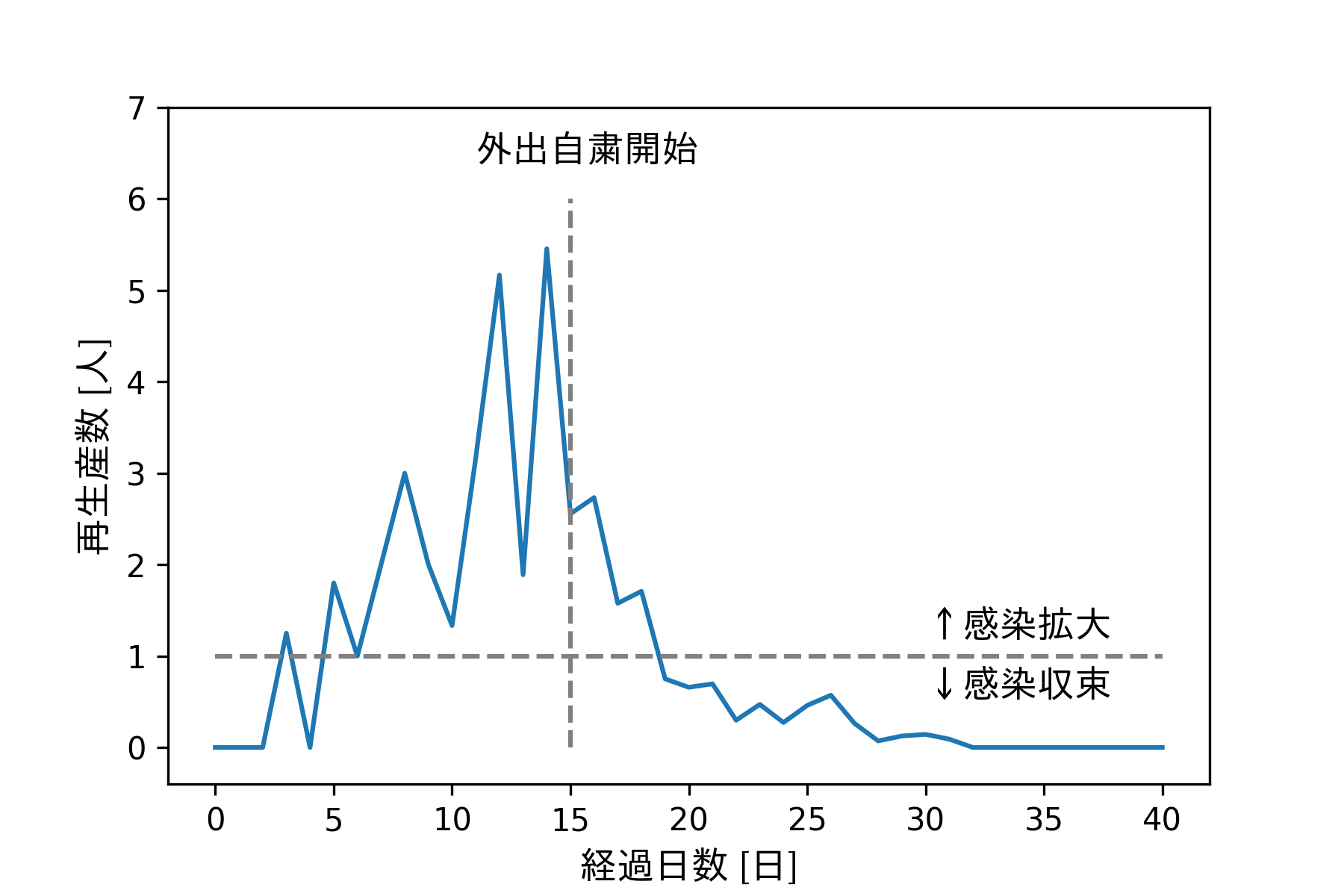
通常の営みを送っている期間、0〜14日の間の実効再生産数は1を超える場合が多く、感染が拡大し続けていることを示しています。一方、15日目に外出自粛が行われた後は急落し、19日目付近で1を下回る結果となりました。すなわち、19日目以降に感染が収束していく傾向が現れたことになります。33日目付近では再生産数が0になり、一人も感染者を出さなくなったことが確認できます。
入院非受理数の時系列変動
当該日に病院へ行ったのに、病床が満床のため、入院できなかった数(医療崩壊の指標)。ここに計上された数が、死亡リスクが高い人々の数であることを示しています。
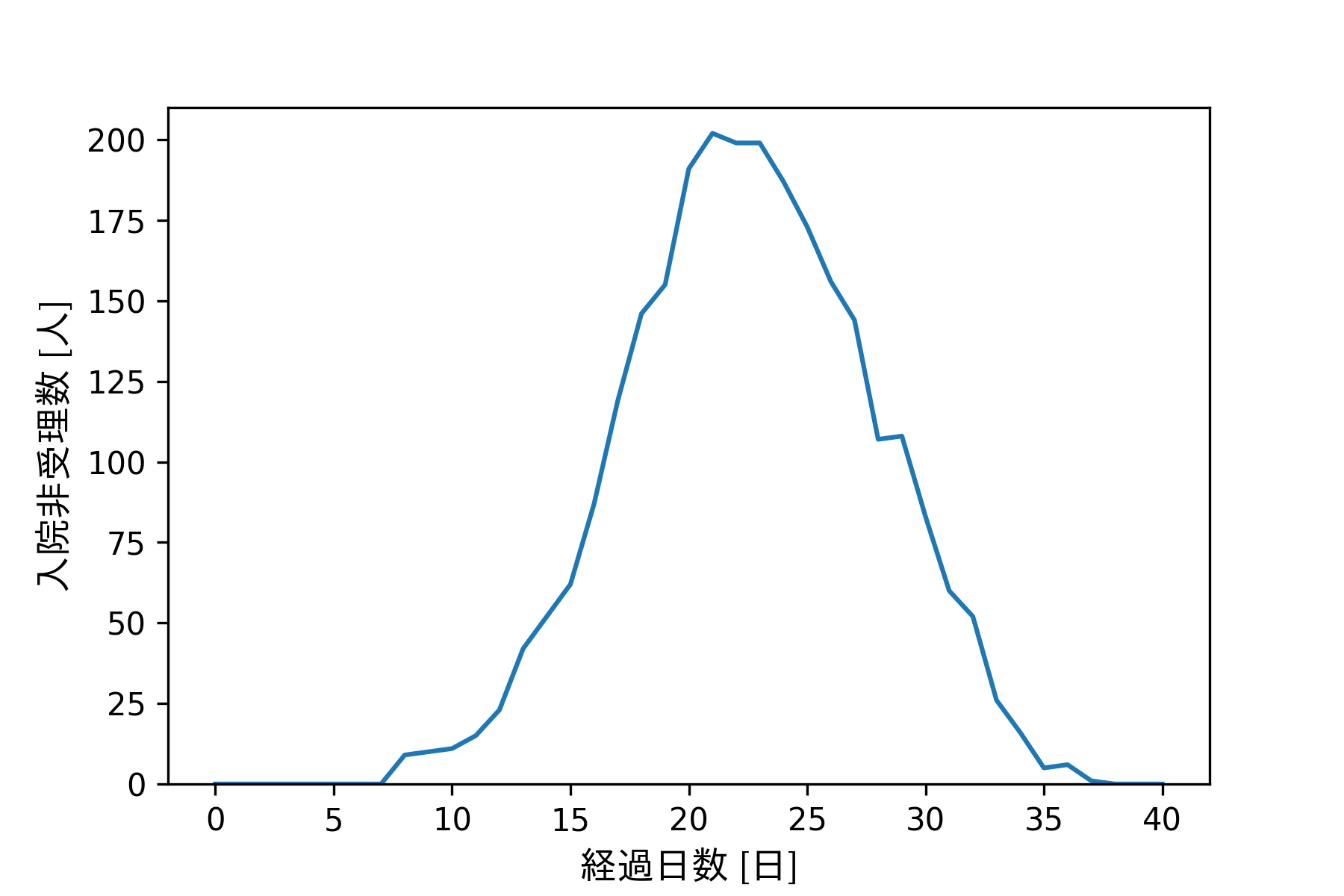
通常の営みを送っている期間であっても、0〜7日の間は非受理が0人ですので、すべての感染者を入院させることができています。一方それ以降は急激に入院非受理数が増加し、20日の時点で200人を迎えます。1650人の社会の1割強に相当する人が病院に殺到して、入院できずに追い出されてしまっているわけです。1日に人口の1割強が高い致死率にさらされるということで、異常事態といえるでしょう。
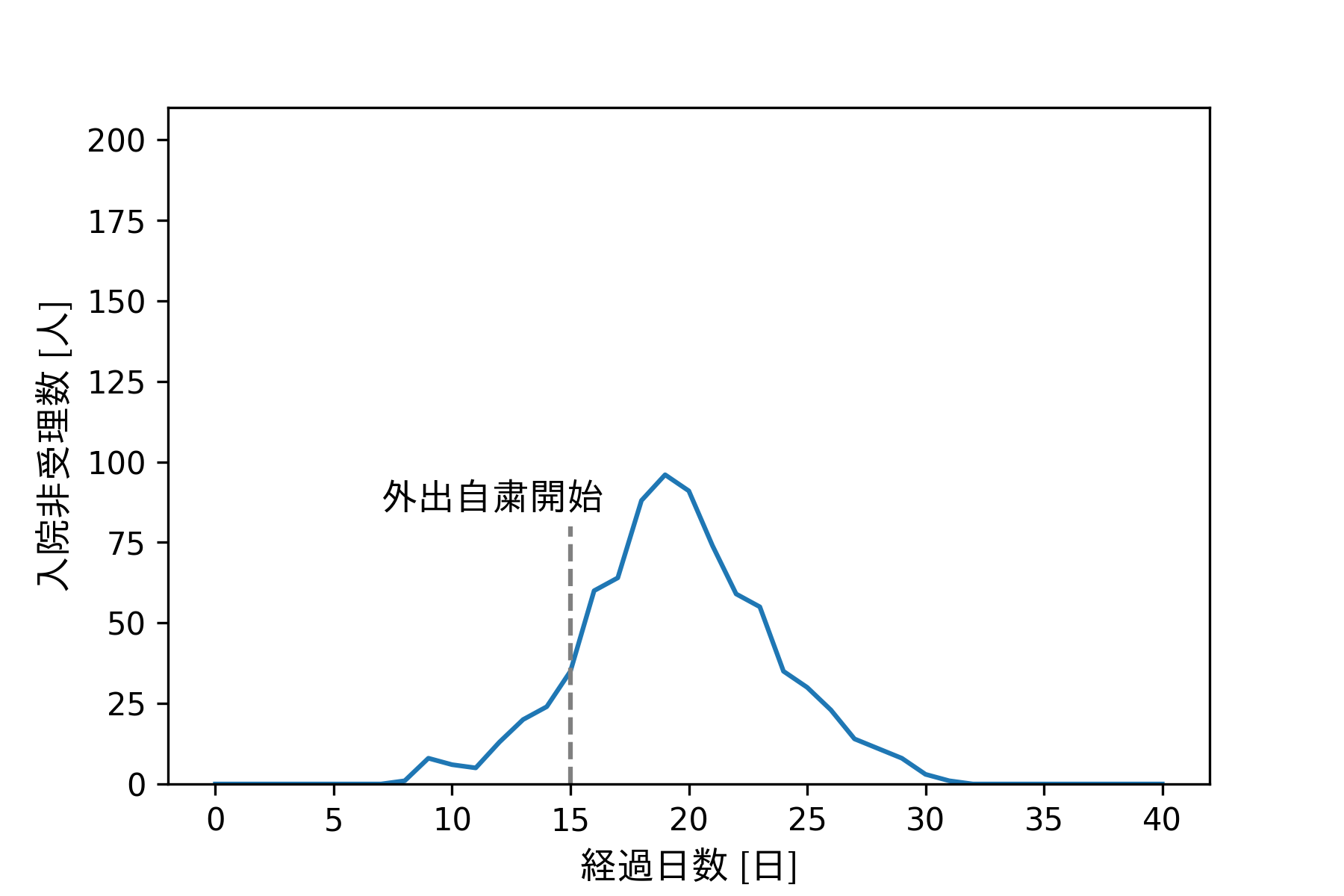
こちらも、0〜7日の間は非受理が0人ですので、すべての感染者を入院させることができています。一方で、8日以降は満床のため非受理数が急激に増加していきます。外出自粛日である15日を経過してもこれが続き、19日目にようやくピークを迎えます。それ以降は徐々に平穏を取り戻します。ピーク自体は外出自粛を行っていない場合と似たような日付ですが、病床不足により入院を拒否した人数はおよそ半分であることがわかります。
まとめ
今回、MASを用いて外出自粛の必要性について論じました。なるべく多くの人が外出を自粛すると、収束も早まるようです。大変だとは思いますが、みんなで頑張っていけるといいですね。ところで、今回は1650人という極めて小規模な人口社会でシミュレーションを行ったので、感染者が0人になっています。1億人近くいる日本国内で、短時間でウイルスを完全に無くすというのはなかなか難しいので、長期戦になるかもしれません。もしワクチンなどができると、健康(I状態)から一気に回復(R状態)に遷移させられますので、非常にありがたいですね。
参考文献
廣瀬, 豊坂, パンデミックシミュレーション, 日本信頼性学会誌, vol.33, pp.270-277, 2009.
今後の方針
python3 でMASのプログラムを書き、matplotlib で描画しました。そのうち公開するかもしれません。追加したい機能としては、偽陽性・偽陰性の影響なども入れてみたいと考えています。またお気付きの方もいるかもしれませんが、乱数のシードが自粛あり/なしで違ってしまっているので、あまりよろしくない比較になっています。そのうち修正するかもしれません。ほか、何か一緒にやりたい方はご連絡ください。
Appendix 細かいパラメータなど
エージェント数: 1650(会社員、主婦/主夫、学生、550人ずつ)
会社員の外出先: 会社(1日0, 1回)
主婦/主夫の外出先: お店(1日0, 1回)
学生の外出先: 学校(1日0, 1回)
外出確率(会社員): 0.99 〜 1.00(一様乱数)
外出確率(主婦/主夫): 0.50 〜 1.00(一様乱数)
外出確率(学生): 0.99 〜 1.00(一様乱数)
外出時刻(会社員): AM8:30 ± 90分(正規乱数)
外出時刻(主婦/主夫): AM10:30 ± 90分(正規乱数)
外出時刻(学生): AM8:30 ± 90分(正規乱数)
外出先滞在時間(会社員):6〜8時間(一様乱数)
外出先滞在時間(主婦/主夫):10〜30分(一様乱数)
外出先滞在時間(学生):5〜6時間(一様乱数)
感染確率/10分接触(状態Sから状態Eへの遷移): 0.0005
非入院死亡確率: 0.10(状態 I 終了後に1回判定)
入院死亡確率: 0.01(状態 I 終了後に1回判定)
感染のとき、入院を求める確率 0.60(1日1回判定)
病床最大数: 15台
感染かつ入院していないとき、外出確率の減少値: 0.30
シミュレーション期間: 40日
初期感染者数: 10人
外出自粛発令日: 15日, なし(2パターン用意)
外出自粛時の外出確率の減少値: 0.80
状態Eから状態Iへの遷移日数: 2, 4, 6日(ランダム選択)
状態Iから状態Rへの遷移日数: 2, 4, 6日(ランダム選択)
会社の座標: [300, 800], [800, 100]
お店の座標: [300, 500], [800, 500]
学校の座標: [300, 100], [800, 800]
活動空間: X->[0, 100], Y->[0, 100]
エージェントの自宅: 活動空間内において一様乱数で生成
感染における接触判定: I 状態(感染者)とのユークリッド距離が1未満
移動距離/10分: 50