1. 前回の復習
For文について学びました。詳細は以下を参照してください。
ワークデザイン02
2. 分散・標準偏差とは?
分散および標準偏差とは、数字の集まりに対して、そのばらつきを示す指標です。最小値は0であり、このとき、数字の集まりはまったくばらつきがない状態を指します。ですので、「分散が0であれば、ばらつきがまったくない!」、「分散が1000であれば、ばらつきがかなり大きい!」ということを意味します(数字はかなりてきとうです)。
皆さんが将来、ある生産ラインの品質管理を行う仕事に就いたとします。物事の改善を行うことが仕事になるわけです。なんらかの改善を行おうとした場合、まず、現状把握を行うことが必要です。この際、生産されてくる製品について、その重さや長さなどのばらつきを算出できるということは非常に重要です。また、なんらかの改善策を講じたときに、ばらつきがどれくらい減ったのか、数値として算出することも重要です。
このようなとき、分散・標準偏差を用いてばらつきを説明します。この単語は、ある水準以上の人間であれば誰でも知っている標準的な用語ですので、きちんとした企業であれば、その用語が上司に通じない、ということは普通ありません。
3. 分散・標準偏差の求め方
ある製品の長さに関する分散・標準偏差は、以下の手続きで求めることができます。
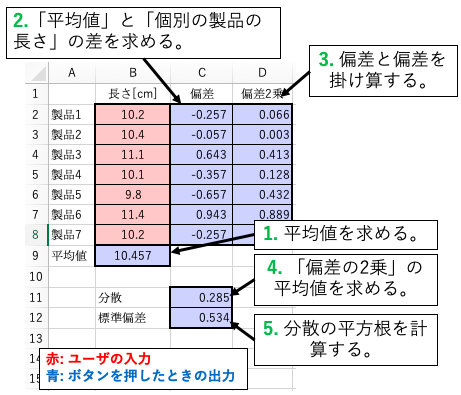
- 製品の長さの平均値を求めます。
- 個別の製品の長さから、平均値を引くことで、個別の製品が有する平均値との差を求めます。これを偏差と呼びます。
- 偏差は個別の製品が有する平均との差ですので、偏差をすべて足すと、製品全体のばらつきになりそうです。ただ、偏差は、平均値より大きいか、平均値より小さいかにより、プラスだったりマイナスだったりします。すると、偏差をすべて足すとプラス側のズレとマイナス側のズレが打ち消し合ってしまいます。これではまずいので、偏差をすべて足す前に、偏差を2乗することで、符号をすべてプラスに統一します。
- これにより、個別の製品の偏差の2乗について、その平均値を算出します。これを分散と呼びます。
- 分散は「個別の製品と平均値の差」を加工した数値なので、平均からどの程度ずれているのか、すなわち「ばらばらな度合い」を示しています。ただ、2乗するという操作があったので、ズレが二乗になってしまっています。そのため、ずれの度合いをより直感的にするために、2乗の情報を取ります。すなわち、分散に対し、その平方根を計算します。これを標準偏差と呼びます。標準偏差は2乗がキャンセルされたばらつきなので、その数値が平均からのずれ、すなわち、ばらつきをダイレクトに表現しているわけです。
4. コード
Private Sub CommandButton1_Click()
Dim A(7) As Double
Dim Dif(7) As Double
Dim Dif2(7) As Double
For i = 1 To 7
A(i) = Cells(i + 1, 2)
Next i
s = A(1) + A(2) + A(3) + A(4) + A(5) + A(6) + A(7)
s = s / 7
Cells(9, 2) = s
For i = 1 To 7
Dif(i) = s - A(i)
Cells(i + 1, 3) = Dif(i)
Next i
For i = 1 To 7
Dif2(i) = Dif(i) * Dif(i)
Cells(i + 1, 4) = Dif2(i)
Next i
d = Dif2(1) + Dif2(2) + Dif2(3) + Dif2(4) + Dif2(5) + Dif2(6) + Dif2(7)
d = d / 7
Cells(11, 3) = d
Cells(12, 3) = Sqr(d)
End Sub
備考1: 平均などを算出するとき、s=A(1)+A(2)+…という書き方は一般に望ましくありませんが、難しくなるのでそのように書いています。
備考2: Sqr(d)とは、dの平方根を求める記述です。
5. 問題(紙のおもて面に記載)
- 分散・標準偏差を求めるには、画像に示したStep 1〜5の手続きが必要です。上にあるコードの何行目から何行目がそれぞれのStepのどれに対応しているか記述してください。例: Step1/4〜10行目、Step2/13〜26行目…
- ある2つの生産ラインにおいて、7個の製品をそれぞれ作成し、重さを測定しました。その結果、重さは以下の通りとなりました。
- ライン1: 10.1g, 9.8g, 11.2g, 10.0g, 8.9g, 8.8g, 9.3g
- ライン2: 11.1g, 9.1g, 10.5g, 10.1g, 10.2g, 8.9g, 9.6g
2つのラインの標準偏差と分散はいくつか。また、どちらのラインの方が良いと言えるか答えてください。
- 構築したソフトウェアを用いて、分散・標準偏差が0になるような7つの製品の長さの組を一つ提示してください。7個の数字を記入すること。0, 0, 0, 0, 0, 0, 0はNGです。
- 分散・標準偏差がマイナスにならない理由を、Step 1〜5を引用しながら、説明してください。(Step nでxxxのためマイナスになり得ない、のような説明です。全Stepを引用する必要はありません)
6. 応用問題(紙の裏面に記載)
12行目と30行目をfor文を使用して記述してください。
(この問題はやらなくてもいいです。取り組み、正しい場合のみ、何点か加点します。)