Abstract
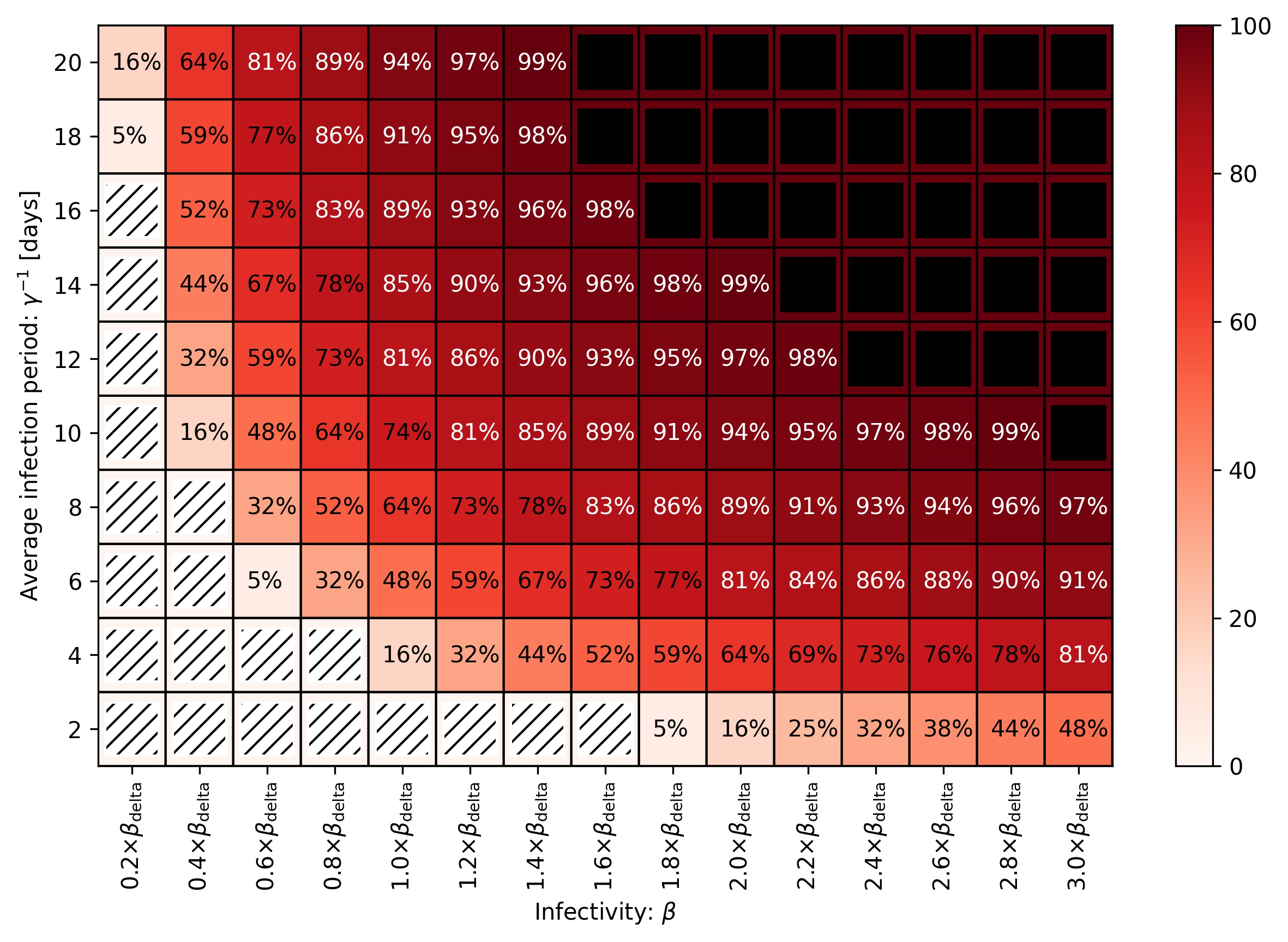
COVID-19は1回目と2回目のワクチン接種の効果が異なるため、いくつかの研究において,1・2回目の接種状態を表現できる様々な数理モデルが開発されている。これらの研究結果により、1・2回目のワクチン接種の影響を考慮した感染症拡大のシミュレーションを行うことができる。しかしこれらはシミュレーションを行うのみであり、その微分方程式の理論的な解析が不十分という問題があった。
そこで,感染者数とワクチン接種者数をパラメータとして,上述の微分方程式を非斉次系に帰着させることで、解析的な近似解を求める方法を提案した。この近似解を用いて、COVID-19 Delta variant(B.1.617)の日本国内における感染者数を減少させるための目標接種率を決定する方程式を作成した。さらに,COVID-19 Delta variant(B.1.617)よりも強い変異体や弱い変異体を持つ場合の目標接種率を算出した。本研究は、SIRVVDモデルの理論的発展に寄与するとともに、COVID-19の感染者数を減少させるための目標接種率に関する知見を提供するものである。
Publication
- Yuto Omae, Makoto Sasaki, Jun Toyotani, Kazuyuki Hara, Hirotaka Takahashi, Theoretical Analysis of the SIRVVD Model for Insights into the Target Rate of COVID-19/SARS-CoV-2 Vaccination in Japan, IEEE Access, vol.10, pp.43044-43054, 2022.04. doi: 10.1109/ACCESS.2022.3168985. [IF: 3.367] [採択率: 30%] [Link]
- Yuto Omae, Yohei Kakimoto, Makoto Sasaki, Jun Toyotani, Kazuyuki Hara, Yasuhiro Gon, Hirotaka Takahashi, SIRVVD model-based verification of the effect of first and second doses of COVID-19/SARS-CoV-2 vaccination in Japan, Mathematical Biosciences and Engineering, vol.19, issue 1, pp.1026-1040, 2022. doi: 10.3934/mbe.2022047. [IF: 2.194] [採択率: 34%] [Link]
Note
この記事および画像は有償サービスにより作成されたものであり、本ページのみでの利用を想定しています。無断利用を発見した場合はご一報ください。