0. はじめに
前回、以下の構成を持つニューラルネットワークを構築しました。
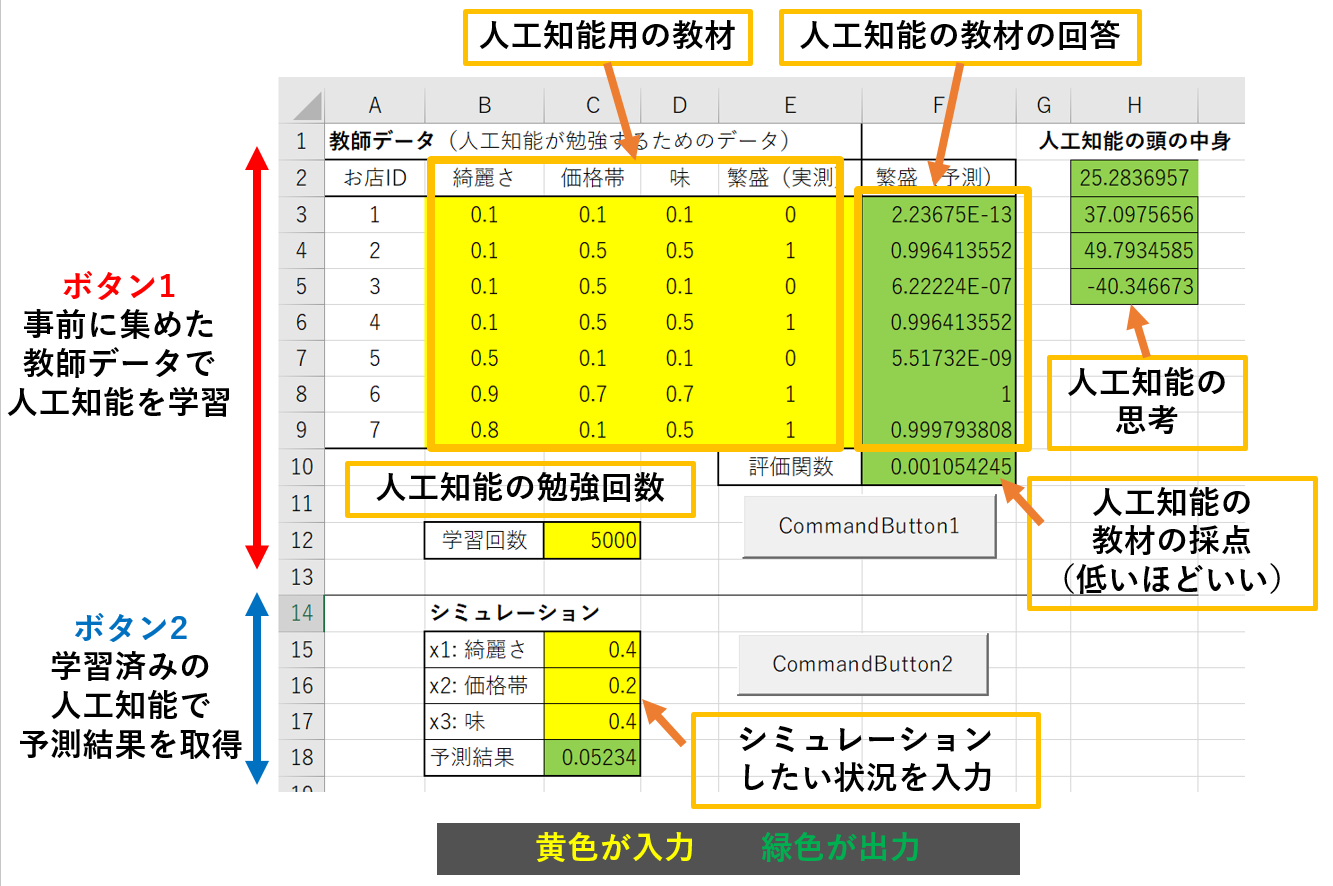
- 入力: x1:綺麗さ、x2:価格帯、x3:味
- 出力: 繁盛しない 〜 繁盛する
- 範囲: 最少0 〜 最大1
0に近いほど悪く、1に近いほど良いことを表します。価格帯は1に近いほど安いことを意味するので、注意してください。
1. 今日やること
今日は、構築した人工知能を使って、いくつかのパターンでシミュレーションしてみます。そして、どのようなお店が一番繁盛しそうなのか、皆さんに考えてもらいます。
2. コード
ボタン1
人工知能に勉強させるボタンです。教師データ(人工知能の勉強用の教材)と、勉強回数を入力すると、学習が開始されます(前回とまったく同じコードです)。
ボタン2
学習させた人工知能に対し、自分がシミュレーションしたい状況を与えて、予測結果を得るボタンです。
ボタン1のコード:
Private Sub CommandButton1_Click()
DataSize = 7
InputDim = 3
Dim W(4) As Double
Dim X(7, 4) As Double
Dim DifW(4) As Double
Dim EstDif(7) As Double
Dim Update(4) As Double
'教師データの取得
For i = 1 To DataSize
For j = 1 To InputDim
X(i, j) = Cells(i + 2, j + 1)
Next j
Next i
'人工知能の学習回数を取得
NumLearning = Cells(12, 3)
'初期のモデルパラメータを決定
For i = 1 To InputDim + 1
Cells(1 + i, 8) = 0
Next i
'勉強開始
For t = 1 To NumLearning
'現在のモデルパラメータを取得
For i = 1 To InputDim + 1
W(i) = Cells(1 + i, 8)
Next i
'現在のパラメータによる予測結果を算出
For i = 1 To DataSize
Est = 0
For j = 1 To InputDim
Est = Est + X(i, j) * W(j)
Next j
Est = Est + W(4)
Est = 1 / (1 + Exp(-Est))
Cells(2 + i, 6) = Est
Next i
'現在のパラメータの評価値を算出
Eval = 0
For i = 1 To DataSize
Eval = Eval + Abs(Cells(2 + i, 5) - Cells(2 + i, 6))
Next i
Eval = Eval / DataSize
Cells(10, 6) = Eval
'頭がよくなる方法を検索
gam = 10
For k = 1 To InputDim + 1
W(k) = W(k) + gam
For i = 1 To DataSize
EstDif(i) = 0
For j = 1 To InputDim
EstDif(i) = EstDif(i) + X(i, j) * W(j)
Next j
EstDif(i) = EstDif(i) + W(4)
EstDif(i) = 1 / (1 + Exp(-EstDif(i)))
Next i
EvalTemp = 0
For i = 1 To DataSize
EvalTemp = EvalTemp + Abs(Cells(2 + i, 5) - EstDif(i))
Next i
EvalTemp = EvalTemp / DataSize
Update(k) = EvalTemp - Eval
W(k) = W(k) - gam
Next k
'モデルパラメータ更新(人工知能の頭の中身を変更)
For i = 1 To InputDim + 1
W(i) = W(i) - Update(i)
Cells(1 + i, 8) = W(i)
Next i
Next t
End Sub
ボタン2のコード:
Private Sub CommandButton2_Click() '学習済み人工知能のパラメータの取得 a1 = Cells(2, 8) a2 = Cells(3, 8) a3 = Cells(4, 8) a4 = Cells(5, 8) '予測したいお店を取得 xn1 = Cells(15, 3) xn2 = Cells(16, 3) xn3 = Cells(17, 3) '予測結果を取得 y = xn1 * a1 + xn2 * a2 + xn3 * a3 + a4 y = 1 / (1 + Exp(-y)) '人工知能の予測結果を書き込み Cells(18, 3) = y End Sub
3. 問題(おもて面に書く)
問題その1:
ニューラルネットワークの勉強回数を5000回とします。この人工知能は、以下のパターンA〜Fのお店に対し、どのような予測結果を示すか、数字を書いてください。
- パターンA
- すごく綺麗だが、価格が高く、味も悪いお店
- x1=0.7, x2=0.1, x3=0.1
- パターンB
- 汚いし、価格も高いが、味が良いお店
- x1=0.1, x2=0.1, x3=0.7
- パターンC
- 汚いが、価格は安い。しかし味が悪いお店
- x1=0.1, x2=0.7, x3=0.1
- パターンD
- 特に特徴がない平均的なお店
- x1=0.3, x2=0.3, x3=0.3
- パターンE
- 全部ダメなお店
- x1=0.1, x2=0.1, x3=0.1
- パターンF
- すべて完璧なお店
- x1=0.8, x2=0.8, x3=0.8
問題その2:
人工知能の学習回数を、10回にして、まったく同じ作業をやってみてください。
問題その3:
学習回数5000回と10回の結果を比較して、学習回数が少ない人工知能の問題点を簡潔に記載してください。
問題その4:
5000回学習した人工知能は、どのような順番でお店が繁盛すると予測するでしょうか。その順番を記載してください。例: AFDECB
ここまで解けたら、提出して帰っていいです。
以下の問題は、加点して欲しい人だけやってください。
4. 応用問題(裏面に書く)
応用問題その1:
基礎問題の方で、学習が少ない人工知能の問題を少し考えてもらいました。しかし、学習させまくれば良いというわけでもありません。学習させすぎた人工知能は、過学習と呼ばれる問題を抱えてしまいます。インターネットで過学習の意味を調べて、簡潔に記載してください。
学習させすぎた人工知能は、人間よりも頭が良くなり、人間を排除しだすとかそういう意味ではありません。
応用問題その2:
いま、あなたはお店を作ろうとしています。しかし、料理があまりうまくないので、「x3: 味」に対し0.3より大きい値をいれることができません。また、まったく掃除をしないというのは許せないので、「x2: 綺麗さ」は0.2以上にすることを心の中で決めています。また、当然ながら繁盛するお店(人工知能の予測が0.8以上)を作りたいと考えています。一方で、できるだけ頑張らずに目標を達成したいので、x1+x2+x3の合計値は限りなく少なくしたいです。これをすべて満たすx1, x2, x3はいくつでしょうか。
このままだとごちゃごちゃしているのでわかりにくいです。この問題を整理すると以下のようになります。
前提条件:
- 人工知能の学習回数は5000回とします。
- 教師データは変更できません。
制約条件:
- 「x3: 味」は0.3より大きな値にできません。
- 「x2: 綺麗さ」は0.2以上にしなければいけません。
- 「人工知能の予測: 繁盛」は0.8以上でなくてはなりません。
問題:
- 「すべての制約条件を違反しない」かつ「x1+x2+x3」が最小となる「x1, x2, x3」の組み合わせを求めよ。
紙に書くこと:
- 自分で探したx1, x2, x3の値(制約違反はアウト!)
- そのときの人工知能の予測結果(制約違反はアウト!)
- x1, x2, x3をすべて足した値(これが小さければ小さいほど良い)
このように、「最適解」を曖昧さが伴わないように定義づけたり、その解を厳密に求める学術分野を、「数理最適化、オペレーションズ・リサーチ」などと言います。興味がある人は調べてみてください。