PyLearnST 08: 共分散構造分析

かなり適当に書いているので後ほど修正するかも 最初に pip3 install semopy をやること

0. はじめに

共分散構造分析とは、重回帰分析で有向グラフを作るような解析手法です。例えば、いま、以下の仮説を有しているとします。

  • よく食べ、よく眠ると、身長が高くなる。
  • よく食べ、よく眠り、身長が高いと、体重が重くなる。

これを以下のように変数化してみます。

  • X1: 食事量
  • X2: 睡眠時間
  • Y1: 身長
  • Y2: 体重

さらにこれを先ほどの仮説に基づいて重回帰分析の形状で表してみると、以下のようになります。

  • Y1 = A X1 + B X2 + e1
  • Y2 = C X1 + D X2 + E Y1 + e2

ここで、A〜Eは分析によって具体的な数字が定まるパラメータ、e1とe2は誤差項となります。誤差項とは、それ以外の要因も考えられるけれど、今回は扱わないという意味を有する変数となります（例えば、Y1身長はX1食事、X2睡眠時間だけではなく、他の要因からも影響を受けますが、全部扱うときりがないので、それは誤差項e1として丸投げするという意味です）。

ところで、上の式を図に書いてみると、以下のようになります。 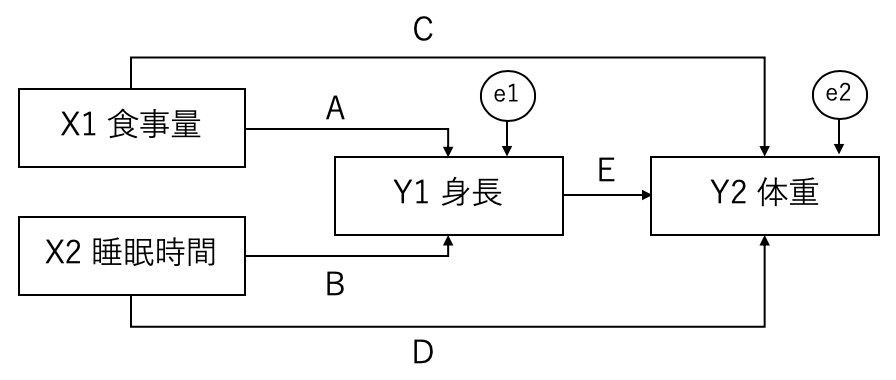もしこのモデルにおいてA〜Eが統計的に有意であり、かつ、実際のデータへの当てはまりが良い場合、はじめに設定した仮説は正しかったと解釈します。

記述のルール： 潜在変数は円や楕円を使用し、観測変数は長方形を使用します。観測変数とは実際に集めることのできるデータによる変数、潜在変数とは観測していない変数となります。誤差項は観測していませんので、潜在変数扱いし、円で囲います。誤差項は何も囲わないとする人もいます。

1. 初期モデルの検証

以下は上の仮説を共分散構造分析で検証するコードです。こちらにサンプルデータがあるので、ダウンロードして実行してみてください。てきとうに作ったデータですので、本当のものではないですから、注意してくださいね。

In [87]:
from semopy import Model

### 変更するのはここだけ ###
# 集めたデータセットのロード
# 注意1: モデルの定義で記載した変数を、csvのヘッダに入れること。
# 注意2: UTF-8形式のcsvファイルでないとエラーになる。
filename = "PyLearnST08sample.csv"

# 仮説モデルの定義
mod = """ Y1_length ~ X1_eat + X2_sleep 
               Y2_weight ~ X1_eat + X2_sleep + Y1_length
      """

### ここから下は特に変更しなくて良い ###
from pandas import read_csv
model = Model(mod)
data = read_csv(filename, index_col=0)
model.load_dataset(data)

# モデルの構築
from semopy import Optimizer
opt = Optimizer(model)
objective_function_value = opt.optimize()

# 結果の出力
from semopy.inspector import inspect
print("### Pass results ###")
print(inspect(opt))
print("")

# モデルの適合度の測定
from semopy import gather_statistics
import numpy as np
stats = gather_statistics(opt)
print("### Fitting index ###")
print("RMSEA = ", np.round(stats[6], 5)) # RMSEA: 0.10以下だと良い
print("GFI = ", np.round(stats[8], 5)) # GFI: 0.90以上だと良い
print("AGFI = ", np.round(stats[9], 5)) # AGFI: 0.90以上だと良い
print("AIC = ",np.round( stats[12], 5)) # AIC: 低いほど良い（相対評価）

### Pass results ###
        lval  op       rval       Value         SE   Z-score   P-value
0  Y1_length   ~     X1_eat    0.599340   1.350035  0.443944  0.657083
1  Y1_length   ~   X2_sleep    4.197183   1.163635  3.606957  0.000310
3  Y2_weight   ~     X1_eat    2.415480   1.174083  2.057332  0.039654
4  Y2_weight   ~   X2_sleep    1.221354   1.449108  0.842831  0.399323
2  Y2_weight   ~  Y1_length    0.506378   0.249015  2.033522  0.042000
5  Y1_length  ~~  Y1_length  140.840464  57.497879  2.449490  0.014306
6  Y2_weight  ~~  Y2_weight  104.799759  42.784322  2.449490  0.014306

### Fitting index ###
RMSEA =  inf
GFI =  0.99999
AGFI =  nan
AIC =  197.36603

色々な結果が出てきました。ここで重要になるのは、ValueとP-valueです。 Valueはパスの係数で、P-valueはその有意性（係数が0である確率なので、低いほど良い）です。これをわかりやすく書くと以下のようになります。

  • X1 から Y1 へのパス係数: 0.599 (P値: 0.657) / 有意でない！
  • X2 から Y1 へのパス係数: 4.197 (P値: 0.000) / 1%水準有意！
  • X1 から Y2 へのパス係数: 2.415 (P値: 0.039) / 5%水準有意！
  • X2 から Y2 へのパス係数: 1.221 (P値: 0.399) / 有意でない！
  • X1 から Y2 へのパス係数: 0.506 (P値: 0.042) / 5%水準有意！

これらを踏まえ、モデルを組んでみると以下のようになります。

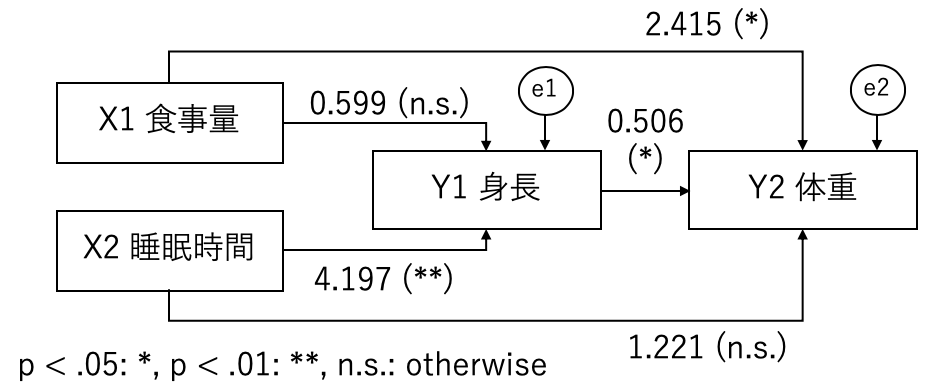
さて、一番下にFitting indexという指標があります。これは、モデルの当てはまりの良さを表す指標で、以下の場合、良いモデルと判断します。

  • RMSEA: 0.10以下
  • GFI: 0.90以上
  • AGFI: 0.90以上
  • AIC: 低いほど良い（モデル同士の相対評価に使用）

これらを踏まえて結果を見てみると、GFIはいい感じがしますが、RMSEAは無限大、AGFIはnanとなり、端的にいうと問題があることを示しています。

2. モデルの改善

さて、上のモデルはあまり良くないと判断されてしまいました。このような場合、仮説の修正を行います。色々な方法がありますが、最もオーソドックスなのは、有意ではないパスを切断するということでしょう。すなわち、X1からY1へ、X2からY2へのパスを切断します。これで再度分析してみましょう。

In [83]:
# モデルの定義
from semopy import Model
mod = """ Y1_length ~ X2_sleep 
               Y2_weight ~ X1_eat + Y1_length
      """
model = Model(mod)

# データのロード
# 注意1: モデルの定義で記載した変数を、csvのヘッダに入れること。
# 注意2: UTF-8形式のcsvファイルでないとエラーになる。
from pandas import read_csv
data = read_csv("PyLearnST08sample.csv", index_col=0)
model.load_dataset(data)

# モデルの構築
from semopy import Optimizer
opt = Optimizer(model)
objective_function_value = opt.optimize()

# 結果の出力
from semopy.inspector import inspect
print("### Pass results ###")
print(inspect(opt))
print("")

# モデルの適合度の測定
from semopy import gather_statistics
import numpy as np
stats = gather_statistics(opt)
print("### Fitting index ###")
print("RMSEA = ", np.round(stats[6], 5)) # RMSEA: 0.10以下だと良い
print("GFI = ", np.round(stats[8], 5)) # GFI: 0.90以上だと良い
print("AGFI = ", np.round(stats[9], 5)) # AGFI: 0.90以上だと良い
print("AIC = ",np.round( stats[12], 5)) # AIC: 低いほど良い（相対評価）

### Pass results ###
        lval  op       rval       Value         SE   Z-score   P-value
0  Y1_length   ~   X2_sleep    4.306812   1.146967  3.754959  0.000173
2  Y2_weight   ~     X1_eat    2.469834   1.185793  2.082854  0.037265
1  Y2_weight   ~  Y1_length    0.657286   0.174426  3.768271  0.000164
3  Y1_length  ~~  Y1_length  143.283425  58.495213  2.449490  0.014306
4  Y2_weight  ~~  Y2_weight  111.010875  45.320000  2.449490  0.014306

### Fitting index ###
RMSEA =  0
GFI =  0.96141
AGFI =  0.90352
AIC =  194.25337

こんな感じでモデルが出来上がりました。先ほどと同じように、図にしてみます。

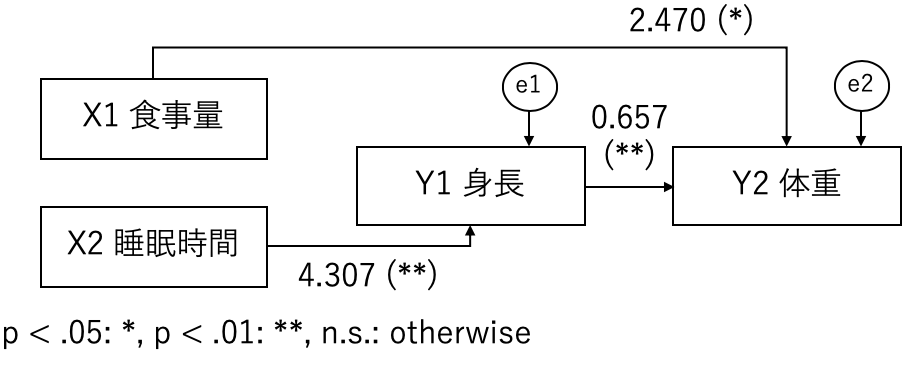
RMSEAが0で、GFI、AGFIは0.90以上です。さらに、AICも先ほどのモデルより低くなっているので、改善が伺えます。以上より、このモデルを良いモデルとみなします。この後は、このモデルや切断したパスから考察を進めていきます。

生き残ったパスより：

  • よく眠ると身長が伸びる！
  • 身長が伸びると体重も増える！
  • ご飯を食べると体重が増える！

切断したパスより：

  • ご飯を食べても身長が伸びない！
  • 眠っても体重は増えない！

生き残ったパスは、まあ妥当な感じですね。切断したパスの「眠っても体重が増えない」のはそりゃそうだという感じがします。一方、「ご飯を食べても身長が伸びない」というのはちょっとおかしい感じもします。などなど、考察を加えていくわけです。

なお前述しているように、本当のデータを使っているわけではないので、今回の結果はてきとうなものであることに留意しておいてくださいね。

Appendix

本稿は、以下のパッケージを利用しています。

その他：

  • 潜在変数を仮定したい場合: 演算子 =~ を使用
  • 共分散（双方向パス）を仮定したい場合: 演算子 ~~ を使用

詳細は上の論文を見ること！