準備¶
本授業では、プログラミング言語pythonを使用します。これは、機械学習、人工知能、統計学といったデータ分析をはじめ、webアプリケーション開発、組込みシステム開発、といったシステム開発まで、とにかくなんでもできる万能なプログラミング言語です。
- 今回はクラウドで動くpython、google colabを使用します。
- ↑ https://colab.research.google.com/
- なので、パソコンとネットワークに接続できるアカウントが必要です。
- 無い人は、タブレットを貸し出します。
実験1. エントロピーの測定と解釈¶
さて、データマイニングを行う上で重要となる概念の一つに、エントロピーというものがあります。エントロピーとは、ものごとの乱雑さや予測のしにくさを測る物差しとして定義されており、以下の特性があります。
エントロピーの特性:
- 状態が予測しにくいほど、値が高くなる。
- 状態が予測しやすいほど、値が低くなる。
- 最小値は0である。
- 物理学において提唱され、データサイエンスの分野で使われるように。
これだけではわかりにくいので、実際にエントロピーを測定してみましょう。
A. 前提条件¶
- 今、袋の中に10個の果物が入っています。
- その果物は、りんご、みかん、どちらかです。
- C1を「りんご」、C2を「みかん」、setを袋とします。
- その内訳には、色々なパターンがありえます。
もし、りんごが9個で、みかんが1個なら、一つ取り出したとき、とても予測しやすいでしょう。一方、もし、りんごとみかんが5個ずつなら、一つ取り出したとき、それが何かは非常に予測がしにくいでしょう。この予測のしにくさをを測定する物差しが、エントロピーとなります。
C1 = "りんご"
C2 = "みかん"
# *** 以下、1つ以外をコメントアウト(#)して実行 ***
Set = [C1, C1, C1, C1, C1, C1, C1, C1, C1, C1] # りんご10、みかん0
#Set = [C1, C1, C1, C1, C1, C1, C1, C1, C1, C2] # りんご9、みかん1
#Set = [C1, C1, C1, C1, C1, C1, C1, C1, C2, C2] # りんご8、みかん2
#Set = [C1, C1, C1, C1, C1, C1, C1, C2, C2, C2] # りんご7、みかん3
#Set = [C1, C1, C1, C1, C1, C1, C2, C2, C2, C2] # りんご6、みかん4
#Set = [C1, C1, C1, C1, C1, C2, C2, C2, C2, C2] # りんご5、みかん5
#Set = [C1, C1, C1, C1, C2, C2, C2, C2, C2, C2] # りんご4、みかん6
#Set = [C1, C1, C1, C2, C2, C2, C2, C2, C2, C2] # りんご3、みかん7
#Set = [C1, C1, C2, C2, C2, C2, C2, C2, C2, C2] # りんご2、みかん8
#Set = [C1, C2, C2, C2, C2, C2, C2, C2, C2, C2] # りんご1、みかん9
#Set = [C2, C2, C2, C2, C2, C2, C2, C2, C2, C2] # りんご0、みかん10
# *** ここから下は変更しなくて良い ***
import numpy as np
import math as mt
NumC1 = 0
NumC2 = 0
for i in range(0, len(Set)):
if Set[i] == C1:
NumC1 = NumC1 + 1
if Set[i] == C2:
NumC2 = NumC2 + 1
ProbC1 = NumC1/len(Set) # りんごの生起確率
ProbC2 = NumC2/len(Set) # みかんの生起確率
if ProbC1 == 0:
ProbC1 = 0.00000001
if ProbC2 == 0:
ProbC2 = 0.00000001
Entropy = - ProbC1 * mt.log2(ProbC1) - ProbC2 * mt.log2(ProbC2)
print(" *** 生起確率 ***")
print("「りんご」の生起確率: ", np.round(ProbC1, 3)*100, "%")
print("「みかん」の生起確率: ", np.round(ProbC2, 3)*100, "%")
print("")
print(" *** エントロピー ***")
print("エントロピー: ", np.round(Entropy, 3))
さて、課題1-1として、
- 横軸: りんごの発生確率、
- 縦軸: エントロピー、
により、測定されたエントロピーを1点ずつプロットしてみてください。 そうすると、
- エントロピーが高いほど、状態が「 」。
- エントロピーが低いほど、状態が「 」。
- 状態が「 」場合、エントロピーは最大を取る。
ということがわかると思います(課題1-2)。
実験2. 決定木によるデータマイニング¶
さて、エントロピーが理解できたところで、それを応用した分析手法、決定木について学習します。決定木とは、「エントロピー最小化」という最適化問題が組み込まれたデータマイニングアルゴリズムにより導出される、状態をきれいに分岐しようとする条件を指します。何を言っているかよくわからないと思うので、具体的な問題を対象に、決定木を立ててみます。
A. 前提条件¶
今回の実験では、どのようなスマートフォンが売れるのか、その条件をデータマイニングによって抽出することを目標とします。このためには、スマホの属性を数値として表現します。そして、その数値がどのような状態のとき、売れるのか、売れないのかを明らかにしていきます。スマホの属性というと、非常に色々な種類がありますが、今回は授業の題材で取り扱うだけですので、シンプルに考えてみます。
入力情報(スマートフォンの属性):
- X0: サイズ(0: 小さい 〜 1: 大きい)
- X1: 価格(0: 安い 〜 1: 高い)
- X2: デザイン性(0: 悪い 〜 1: 良い)
出力情報(売行き):
- Y = C1: 売れる
- Y = C2: 売れない
つまり、サイズ、価格、デザイン性の3要素がどのような条件を満たしたとき、売れるのか、売れないのか、このルールを抽出していくわけです。
B. 教師データ¶
さて、これを実現するには、データが必要です。決定木は機械学習により構成されるので、教師データがなければ何も始まりません。今回、以下に示す色々なスマートフォンを10個用意してみました。そしてそれが、売れるのか売れないのか、調べてみた結果を示します。
# X0: サイズ
X0 = [0.7, 0.6, 0.3, 0.2, 0.7, 0.8, 0.9, 0.8, 0.7, 0.6 ]
# X1: 価格
X1 = [0.4, 0.2, 0.6, 0.8, 0.7, 0.9, 0.8, 0.6, 0.7, 1.0 ]
# X2: デザイン性
X2 = [0.1, 0.9, 0.8, 0.1, 0.8, 0.9, 0.9, 0.2, 0.3, 0.1 ]
# Y: 売れ行き
C1 = "C1: 売れる"
C2 = "C2: 売れない"
Y = [C1, C1, C1, C1, C1, C1, C2, C2, C2, C2]
print("### 教師データ ###")
print("")
for i in range(0, len(Y)):
print(" ***", str(i), "番目の観測 ***")
print(" X0: サイズ = ", X0[i], " / X1: 価格 = ", X1[i],
" / X2: デザイン性 = ", X2[i], " ならば Y = ", Y[i])
print("")
価格が0.3とは一体いくらなんだ?という疑問もあるかと思いますが、今回はこちらで用意した模擬的なデータですので、0ならとても安い、1ならとても高い、くらいの感覚で捉えてください。
それでは、これを実際に観測されたデータとみなし、決定木によるデータマイニングを行ってみます。
from sklearn import tree
import numpy as np
# データ整形
X = np.zeros([len(Y), 3])
for i in range(0, len(Y)):
X[i, 0] = X0[i]
X[i, 1] = X1[i]
X[i, 2] = X2[i]
# 決定木の学習
TreeModel = tree.DecisionTreeClassifier(criterion='entropy', min_samples_leaf=2,
random_state=3)
TreeModel = TreeModel.fit(X, Y)
# 得られたモデルの可視化
import pydotplus
dot_data = 'Tree.dot'
tree.export_graphviz(TreeModel, out_file=dot_data) # モデル入力
graph = pydotplus.graphviz.graph_from_dot_file(dot_data)
graph.write_png('Tree.png') # pngで保存
graph.write_pdf('Tree.pdf') # pdfで保存
# jupyterで表示
print("*** 参考 ***")
print("X0サイズ(0小さい〜1大きい)")
print("X1価格(0安い〜1高い)")
print("X2デザイン性(0悪い〜1良い)")
print("value: 売れる数、売れない数")
from IPython.display import Image
Image(graph.create_png())
さて、得られた木を、下図右側のように、わかりやすい図に変換してみてください(課題2-1)。また、ルートノードとリーフノードの意味も、自分なりに考察してみましょう。
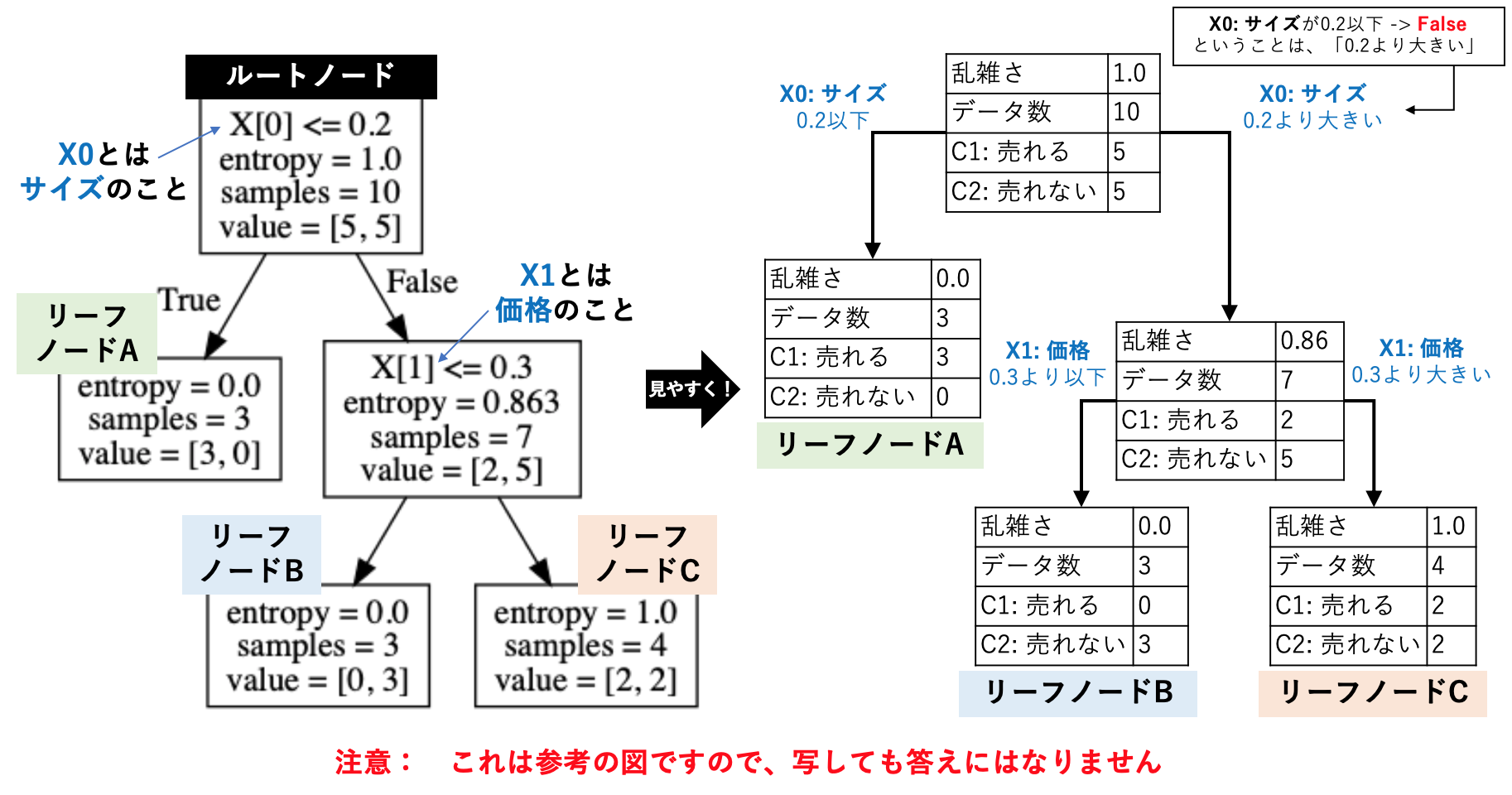
得られた木構造は「どういうとき、どうなるか」という論理的なルールと対応しています。上に示した木の構造と下のルール抽出例をみて理解できたら、出来上がった木からルールの抽出を行なってください(課題2-2)。

これができた人は、課題2-3を行います。決定木は、ルートノードに近い浅い位置にある条件ほど、重要という解釈を行います。データマイニングにより得られた結果から、スマホの売れ行きに重要な要因を「サイズ、価格、デザイン性」の中から、重要度の順番で記載してください。
さて、木構造は条件付き確率を導出するネットワークとみなすこともできます。スマホの属性がいかなる条件を満たすとき、売れる確率がどのくらいなのか、木構造をよくみて考えてみてください(課題2-4)。パーンセント単位で答えること(0%, 10%, 33.3%...など)。
- (a) サイズ、価格、デザイン性、何も情報がない製品
- (b) 価格が安い製品
- (c) 価格が高い製品
- (d) 価格が高く、サイズが小さい製品
- (e) 価格が高く、サイズが大きくい製品
- (f) 価格が高く、サイズが大きく、デザイン性が悪い製品
- (g) 価格が高く、サイズが大きく、デザイン性が良い製品
続いて、課題2-5を行います。この課題は、表に示す様々な製品に対して、構築した木は、「売れる」、「売れない」いずれの判断を行うか、まとめてみてください。
課題2-1〜2-5を通して、決定木によるデータマイニングはどのような事実を明らかにすることが可能な分析手法か、自分なりに考察してみてください(課題2-6)。
最後に、課題2-7です。 ルートノードは、データを一切分割していない状態を表します。そして、リーフノードは、データをできるだけ予測しやすいようにきれいに分割した状態を表します。
- (1) ルートノードのエントロピーを答えよ。
- (2) リーフノードのエントロピーの平均値を求めよ。
- (3) この決定木は、エントロピーをいくら削減したか、求めよ(1から2を引けばok)。
- (4) 今、エントロピーをたくさん削減できる決定木と、あまり削減できない決定木がある。どちらの木が優秀か、理由とともに記載せよ。
これらの問題をきちんと理解すると「エントロピーの削減量を最大化する分岐規則」こそが、「機械学習における決定木の構築方法」ということが理解できると思います。
はやくおわった方:¶
授業外課題(課題3)をやっててください。
課題3-1¶
「決定木におけるオッカムの剃刀」とは何か。調べてください。
課題 3-2¶
あなたであれば、決定木によるデータマイニングを活用して、どのような課題を解決しますか。レポート用紙に以下を記載してください。厳密であるほど、加点します。他の人では考えないような斬新なものほど、加点します。
- 対象とする課題(今回でいえば、「売れるスマホの属性を明らかにする」)、
- 入力変数(今回でいえば、サイズ、価格、デザイン性)、
- 出力変数(今回でいえば、スマホが売れる、売れない)
- 想定される決定木(自分で予想してok、プログラムは不要)
- 木構造からわかること、あなた自身の考察
課題3-3¶
りんごの生起確率をa、みかんの生起確率をbとしたとき、実験1で算出しているエントロピーはいかなる式で求めたものか、その式を記載してください。プログラムを読み解いてもいいですし、webで調べてみてもいいです。webで調べる場合は、情報エントロピーで検索してください。ただのエントロピーで検索すると、物理の難しい式が出てくるかも。どうしても数学が嫌な人は、ここは空欄でもいいです。
備考:¶
今回の資料も、様々な動機、学力の人向けに作った資料ですので、なるべく簡単にしています。したがって、厳密さに欠ける望ましくない説明もいくつかあります。今回の授業で興味を持って、データサイエンスを専門にしたいと思うようになった方は、もうちょっと詳しい資料で詳細に勉強してみてください。