準備¶
本授業では、プログラミング言語pythonを使用します。これは、機械学習、人工知能、統計学といったデータ分析をはじめ、webアプリケーション開発、組込みシステム開発、といったシステム開発まで、とにかくなんでもできる万能なプログラミング言語です。
- 今回はクラウドで動くpython、google colabを使用します。
- ↑ https://colab.research.google.com/
- なので、パソコンとネットワークに接続できるアカウントが必要です。
- 無い人は、タブレットを貸し出します。
A. 前提条件¶
いま私たちは、あるチェーン店の商品を管理する部門にいるとします。この部門では、効率の良い経営のために、需要と供給のバランスを調整することが重要と考えています。すなわち、明日の来客数を事前に予知しておくことが重要になります。
「来客数」を予想するためには、前の日に予報される「降水確率」と「予想気温」が重要なのではないかと考えました。すなわち、
- 入力
- X1: 降水確率(前日に知ることができる)
- X2: 予想気温(前日に知ることができる)
- 出力
- Y: 来客数(当日にならないと知ることができない)
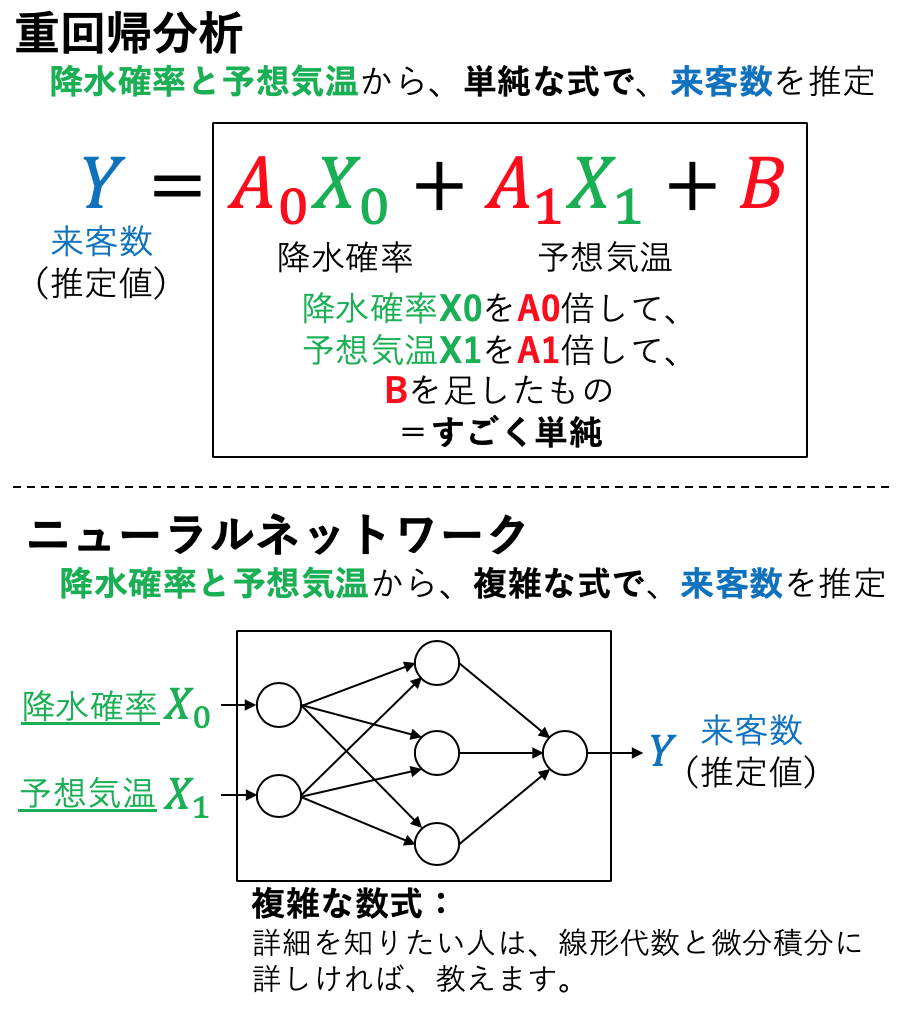
という予測モデルを構築します。このため、
- 重回帰分析
- ニューラルネットワーク
という2つの分析を例にとり、実際にモデル構築を行なっていきます。
B. 教師データ¶
機械学習において人工知能を構築する際、
- 教材にある問題を解く
- 正答率を出す
- 思考を変える
- 1に戻る(これを何度も繰り返す)
- 教材の問題をよく解けたら、未知の問題も解けるんじゃないの?
という過程を踏みます(すべての手法がこれを満たすわけではありませんが)。これを成すには、教材が必要になります。そして、その正答率を知らねばいけませんから、正解が何なのかも教えてあげなくてはいけません。
これを今回の問題に当てはめてみると、
- 教材
- 問題: 降水確率と予想気温
- 答え: 来客数
という、問題と答えがセットになった教材が必要になることを意味しています。「降水確率が20%、予想気温が30度のとき、500人のお客さんが来た」という事例を、たくさん集めなければいけません。
そして、降水確率と予想気温を教えてあげたとき、知能は、来客数を予想します。これがどれくらい間違っていたのか教師が教えてあげます。間違えた度合いを知った知能は、思考を修正して、もう一回、教材の問題に取り組むわけです。
このように、実際にデータを集め、問題と答えがペアになった教材を作ってあげなくてはいけません。このデータは、教師が教材の問題を採点するという構造になっているので、教師データと呼びます。
今回は、以下の教師データが集められたことを想定します。実際にみなさんが何か人工知能を作りたいときは、自分で集めなくちゃいけません。
実行結果が出たら、プリントの表に埋めてみましょう。
# 降水確率
X1 = [0.1, 0.5, 0.9, 0.1, 0.1,
0.9, 0.9, 0.3, 0.7, 1.0 ]
# 予想気温
X2 = [0.4, 0.4, 0.4, 0.1, 0.9,
0.1, 0.9, 0.3, 0.7, 1.0 ]
# 来客数
Y = [0.91, 0.62, 0.21, 0.63, 0.61,
0.12, 0.09, 0.31, 0.32, 0.01 ]
print("### 教師データ ###")
print("")
for i in range(0, len(Y)):
print(" ***", str(i), "番目の観測 ***")
print(" X1: 降水確率 = ", X1[i], " / X2: 予想気温 = ", X2[i], " ならば Y: 来客数 = ", Y[i])
print("")
なお、諸般の事情により、最小0、最大1に規格化しています。元に戻したい場合は、以下の式に当てはめてください。
- 降水確率: 100倍する。(0.5 -> 50%)
- 予想気温: 20倍して、15を足す。(0.5 -> 10 + 15 = 20度)
- 来客者数: 1000倍する。(0.5 -> 500人)
from sklearn.linear_model import LinearRegression
import numpy as np
# データセットの整形
X1 = np.reshape(X1, (len(X1), 1))
X2 = np.reshape(X2, (len(X2), 1))
X=np.concatenate([X1, X2], 1)
# 重回帰分析による回帰式の学習
ModelLR = LinearRegression()
ModelLR.fit(X, Y)
# 結果表示
print("### 重回帰分析による予測モデル ###")
print('y^ = ', round(ModelLR.coef_[0], 2),' X1 + ',
round(ModelLR.coef_[1], 3) ,'X2 + ',
round(ModelLR.intercept_, 3))
print("")
print("*** パラメータ ***")
print("Y^: 予測された来客者数")
print("X1: 降水確率")
print("X2: 予想気温")
print("")
print("### 重回帰分析による予測結果 ###")
Y_LR = ModelLR.predict(X)
for i in range(0, len(Y)):
print(str(i), "番目の予測= ", str(np.round(Y_LR[i], 2)), "(参考: 実測=", Y[i], ")")
#print("")
#print("平均二乗誤差: ", np.mean(np.abs(Y_LR-Y)))
結果が出たら、課題1-1を解いてください。「重回帰分析による予測結果」は、教材(教師データ)に対する予測結果を表しています。二乗誤差というのは、「正しい答え」から「予測された値」を引き算し、それを二乗した値となります。
課題1-1が終わった後は、課題1-2を解いてみてください。
課題1-1, 1-2から、重回帰分析のメリット・デメリットが見えてきます。
- 予測モデルの式がシンプルであるがゆえに...
- デメリット: 予測精度はそこまで高くならない。
- メリット: 入出力間の関係が明瞭に考察できる。
ニューラルネットワークによる予測モデルの構築¶
続いて、ニューラルネットワークと呼ばれる手法で、予測モデルを立ててみます。
from sklearn.neural_network import MLPRegressor
# ニューラルの定義
NNmodel = MLPRegressor(
hidden_layer_sizes=(3, ),
solver='adam',
activation="logistic",
learning_rate_init=0.01,
random_state=1,
max_iter=5000,
tol = pow(10, -100),
verbose=False)
# ニューラルの学習開始
NNmodel.fit(X, Y)
# 結果表示
print("### ニューラルネットワークによる予測モデル ###")
print("複雑な数式なので、省略します。")
print("")
print("### ニューラルネットワークによる予測結果 ###")
Y_NN = NNmodel.predict(X)
for i in range(0, len(Y)):
print(str(i), "番目の予測= ", str(np.round(Y_NN[i], 2)), "(参考: 実測=", Y[i], ")")
#print("")
#print("平均二乗誤差: ", np.mean(np.abs(Y_NN-Y)))
結果が出たら、課題1-3を解いてみましょう。
どんな学習が行われた?¶
さて、ニューラルネットワークの場合、重回帰分析とは異なり、得られる式が極めて複雑なので、その式の形からモデルの構造を考察するということができません。ただし、降水確率と予想気温を、0.01刻みずつ増やし、予測結果を得て、それをヒートマップで可視化することで、入出力関係を考察することができます。以下に、そのコードを示します。
# メッシュデータ生成
Xmin, Ymin, Xmax, Ymax = 0, 0, 1, 1 # 空間の最小最大値
resolution = 0.01 # 細かさ
x_mesh, y_mesh = np.meshgrid(np.arange(Xmin, Xmax, resolution),
np.arange(Ymin, Ymax, resolution))
MeshDat = np.array([x_mesh.ravel(), y_mesh.ravel()]).T
# メッシュデータの推定
z = NNmodel.predict(MeshDat)
# データ整形
z = np.reshape(z, (len(x_mesh), len(y_mesh)))
# 可視化
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(7, 6))
plt.pcolor(x_mesh, y_mesh, z, cmap="hot")
plt.colorbar()
plt.title('visualization', size=15)
plt.xlabel('X1: Rain', size=15)
plt.ylabel('X2: Temperature', size=15)
plt.show()
横軸がX1降水確率、縦軸がX2予想気温、色の濃淡が来客者数を表しています(白いほど人が来る、黒いほど来ない)。X1、X2、Yの間には、どのような関係があるでしょうか?可視化されたニューラルネットワークの入出力関係から、自由に考察してください(課題1-4)。
このように可視化することができるわけですが、これができるのは、入力が2つの場合だけです。現実的に精度の高い予測モデルを目指す場合、入力は2つではなく、10個、100個とたくさん必要なわけです。そういう場合、可視化は当然できません。したがって、ニューラルネットワークで入出力間の関係を考察することは難しいことがわかります。予測精度は高くなりやすいんですけどね。
ニューラルネットワークについてまとめると、
- 形成される知能を構成する式が複雑なので...
- メリット: 精度の良い予測が行えやすい。
- デメリット: 入出力間の関係を考察することが難しい。
実験2. グリッドサーチによるニューラルネットワークの最適化¶
続いて、知能の勉強方針を変えてみて、それが精度にどのような影響をもたらすか、調べてみたいと思います。これを変化させる方法はたくさんありますが、今回は以下の2つを変化させてみることにします。それぞれ、以下の意味があります(課題2-1)。
- 学習回数: 人工知能の思考を何回変化させるか
- 学習係数: 一回の学習に対する、変化の大きさ
以下に、学習回数と学習係数を変化させたニューラルネットワークと、その平均二乗誤差を算出するコードを示します。学習係数と学習回数を変化させながら、別紙の表を埋めてみましょう(課題2-2)。このように、知能を構成する変数をちょっとずつ変化させ、精度を求め、最適なモデルを探す行為を、機械学習の分野ではグリッドサーチと呼びます。
# *******ここを変化させる *******
NumLearning = 1 # 学習回数
LearningRate = 0.1 # 学習係数
# *******この下は変化させない *******
# ニューラルの定義
NNmodel_ex2 = MLPRegressor(
hidden_layer_sizes=(3, ),
solver='adam',
activation="logistic",
learning_rate_init=LearningRate,
random_state=1,
max_iter=NumLearning,
tol = pow(10, -100),
verbose=False)
# ニューラルの学習開始
NNmodel_ex2.fit(X, Y)
print("### ニューラルネットワークによる予測結果 ###")
Y_NN_ex2 = NNmodel_ex2.predict(X)
for i in range(0, len(Y)):
print(str(i), "番目の予測= ", str(np.round(Y_NN_ex2[i], 2)), "(参考: 実測=", Y[i], ")")
print("")
print("平均二乗誤差: ", np.mean(np.abs(Y_NN_ex2-Y)))
表がすべて埋め終わった後は、表を眺めながら、学習係数と学習回数は、ニューラルネットワークの精度にどのような影響をもたらすか、自由に考察してください(課題2-3)。
まとめ¶
今回の実験では、ものごとを予測する基本として、機械学習を扱いました。この中で、シンプルな式により予測を行う重回帰分析と、複雑な式で予測を行うニューラルネットワークを取り扱いました。どちらも予測を実現することが可能ですが、お互い対照的なメリット・デメリットを保持しています。
今回は、学術的な厳密性よりもわかりやすさを優先させています。したがって、学術的に見れば不適切な説明がいくつかあります。もし、データサイエンスや人工知能を専門にしたい人は、自分できちんと学習することを期待します。おかしいところを突っ込んでくれると、嬉しいですね。
早く終わった方へ:¶
授業外課題に取り組んでください。
課題3-1 機械学習・人工知能の分野では、以下の用語が頻出する。それぞれどのような意味を持つか、記述せよ。数式などは記載しなくて良い。意味のわからない専門用語は用いず、自分の理解できる言葉のみ使用すること。
- 回帰問題(Regression)
- クラス分類問題(Classification)
- 訓練誤差(Training error)
- 汎化誤差(Generalization error)
- 次元の呪い(Curse of dimensionally)
課題3-2 機械学習や統計学を実施する上で、よく使われるプログラミング言語を調査せよ。
課題3-3 今、社会や経営に存在する何らかの問題を解決したいとする。この問題を自分で考え、解決につながる予測モデルを提案せよ。回答に際しては、以下の点を記載すること。
- どのような問題を解決したいか。
- 提案した予測モデルの入力と出力は何か。
- 重回帰分析、ニューラルネットワーク、どちらを使用すべきか。理由含む
- 回帰問題か、クラス分類問題か。